Fingering and Unstable Flows

Preferential flow refers to a rapid flow of water in the upper layers of soil along the small cracks or pathways or due to natural soil heterogeneity. Gravity-driven finger flows represent one form of preferential flow that occurs in vadose zone mainly because of instability of gravity-driven flow. We tested three models on ability to represent fingering in soils: the conventional Richards equation, the sharp front Green-Ampt model, and the non-equilibrium relaxation model.

Richards equation

The Richards equation accommodates equilibrium functional relationships between capillary pressure and saturation and presents a conventional approach for solving problems in the vadose zone. The model can be presented as: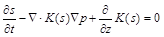

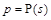
We proved that the solution developed with the Richards equation cannot mimic unstable flows in unsaturated zones and thus unsuitable for fingering.

Non-equilibrium relaxation model

The results that proved that any solution of the Richards equation was unconditionally stable showed that the conventional model must be modified to be able to describe fingering phenomena in unsaturated porous media. One possible extension of the Richards equation takes into account dynamic memory effects by adding a mechanism of relaxation in the relation between water saturation and capillary water pressure. The non-equilibrium model does not change mass balance equation, but replaces the pressure relationship with the kinetic relation for dynamic water pressure:

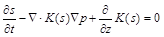
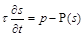
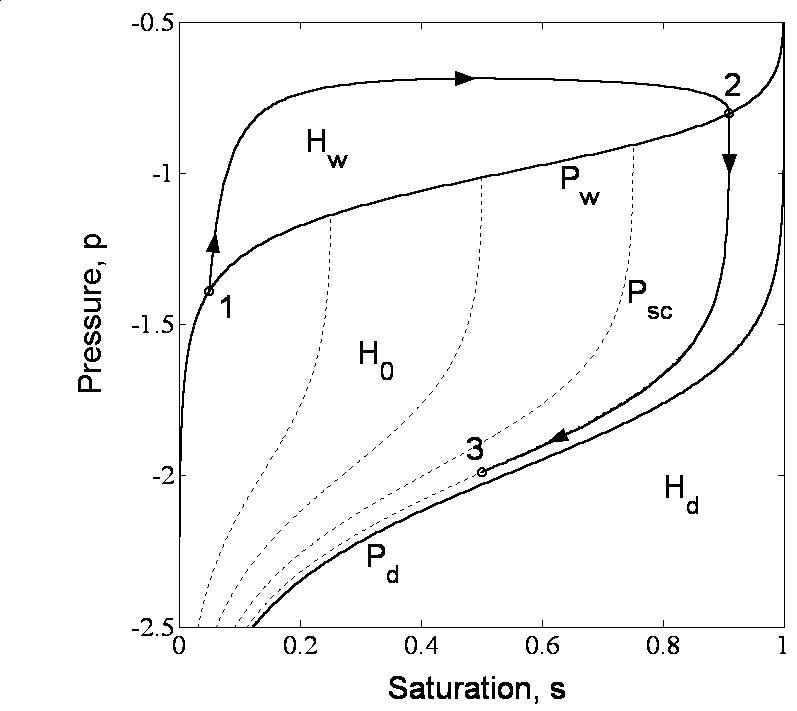
A typical closed-loop hysteresis diagram shown here presents trajectories of one-dimensional infiltration with the relaxation model. The dashed lines represent the scanning drainage curves. The trajectory of the process follows points 1 (initial state), 2 (switching point), and 3 (final state).

This non-equilibrium model accompanied by hysteresis in capillary pressure-saturation relationship was numerically proved to be capable of initiating finger growth and further containing its persistent progression downward. The study of gravity-driven infiltration and stability of wetting fronts involved analytical stability analysis and one- and two-dimensional numerical modeling. Numerical formulation for the gravity-driven infiltration problem and the obtained results provide the evidence that the non-equilibrium model can be used to describe fingering.

Numerical simulations

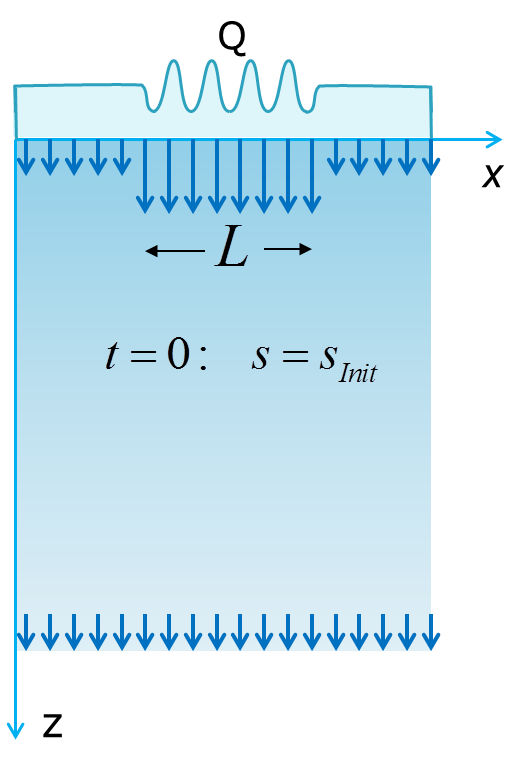
Numerical simulations were conducted for the 2-D rectangular domain with the infiltration flux applied to an upper boundary over the length L. The infiltration flux was perturbed with a sinusoidal function. To assure that the process studied is a two-stage wetting-drainage process, the uniform gravity-driven background flux was maintained over both the lower boundary and the portion of the upper boundary outside of the infiltration source.

Experiments with the infiltration intensity and the length of the applied infiltration source showed various numbers of fingers produced with different values of infiltration length, finger moving rates, finger tip saturation, etc.

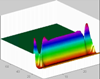
Single Finger

The morphology of the single finger is defined by three distinct features: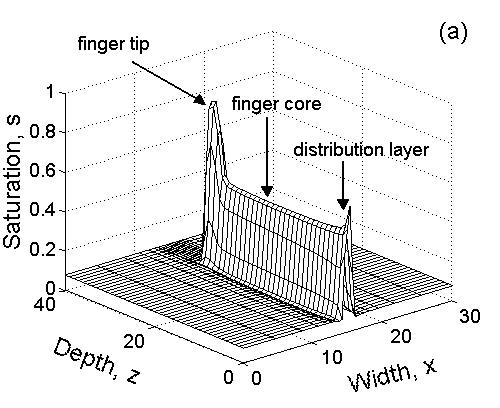

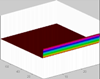
The finger tip has a higher water saturation, stationary finger core and a distribution layer.

Once developed the distribution layer remains steady while the tip of the finger moves at a constant velocity without change in shape and the finger core length grows at a steady rate. The distribution layer provides a steady water flux into the finger core.

Lateral spreading of the finger core is halted by the pressure inside the finger being smaller than the background pressure.

Moisture distribution for the advancement of a single finger:

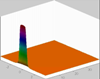
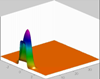
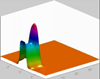
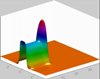
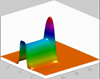
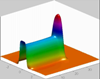
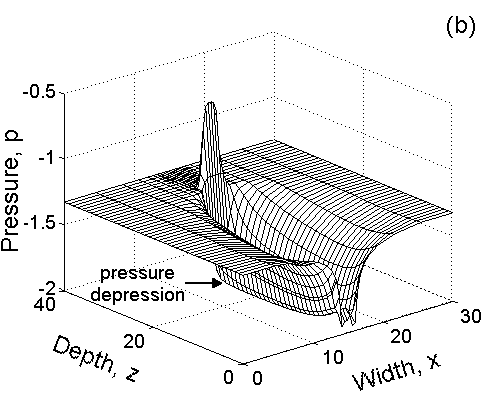
Pressure distribution for the advancement of a single finger:

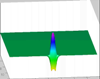
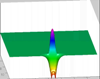
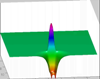
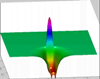
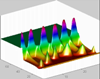
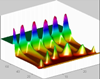
Multiple Fingers

By increasing the length of the infiltration source an increasing number of fingers forms. The width and velocity of individual fingers are affected by the length L. For multiple fingers the flow breaks into more than one fingers. These fingers first formed at different depths as the infiltrating front moved downward. The tips of the fingers are at a lower saturation, and the saturation within the finger cores is significantly lower than the core saturation observed in the single finger case. The total applied flux is split among the fingers, but not uniformly. The distribution layer focuses the applied flux to the different fingers in a manner that does not produce an equal partitioning of the flux to the fingers. The fingers required more than twice the time to reach the depth of the domain compared to the single finger case where all of the flux was concentrated into one finger.

Moisture distribution for the advancement of multiple fingers:

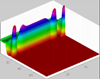
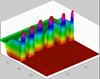
Pressure distribution for the advancement of multiple fingers:

Relevant publications:

1. Nieber. J., R. Dautov, A. Egorov, and A.Y. Sheshukov (2005) Dynamic capillary pressure mechanism for instability in gravity-driven flows; Review and extension to very dry conditions, Transport in Porous Media, 1-2, 151-172. 
2. Nieber, J., A. Sheshukov , R. Dautov and A. Egorov (2003) Non-equilibrium model for gravity-driven fingering in water repellent soils: Formulation and 2-D simulations, in Book: Soil water repellency: Occurrence, Consequences and Amelioration, Elsevier, Ch. 23, 245-258.
3. Egorov, A., R. Dautov, J. Nieber, and A.Y. Sheshukov (2003) Stability analysis of gravity-driven infiltrating flow, Water Resources Research, 39, 1266, DOI:10.1029/2002WR001886. 
4. Dautov, R., A. Egorov, J. Nieber, and A.Y. Sheshukov (2002) Simulation of two-dimensional gravity-driven unstable flow. In: Proceedings of 14th International Conference on Computational Methods in Water Resources, Delft, The Netherlands, 1, 9-16. 
5. Egorov, A., R. Dautov, J. Nieber, and A.Y. Sheshukov (2002) Stability analysis of traveling wave solution for gravity-driven flow. In: Proceedings of 14th International Conference on Computational Methods in Water Resources, Delft, The Netherlands, 1, 120-127.